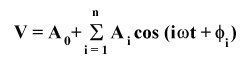
Fourier coefficients are terms found by fitting a periodic sequence to a sin and/or cosine function.
In the case of variable stars, the current form of the Fourier fitting formula was introduced by
Simon and Lee (1981), who used the formula
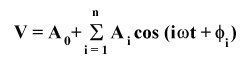
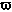 is 2
is 2  /period.
The coefficients are the Ai terms and
the
/period.
The coefficients are the Ai terms and
the 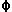 i terms.
i terms.
The Ai terms and
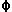 i terms are often combined to
produce useful values,
i terms are often combined to
produce useful values,
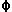 ij =
ij =
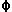 i - i
i - i 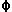 j
j
The Rij and 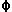 ij values are valuable
in discerning various aspects of stellar properties. These include pulsation mode, resonance effects, metallicity effects,
temperature, and luminosity values. Fourier coefficients have been derived for a wide variety of stars, including
Cepheids, RR Lyrae, Delta Scutis, Miras and SX Phe stars.
ij values are valuable
in discerning various aspects of stellar properties. These include pulsation mode, resonance effects, metallicity effects,
temperature, and luminosity values. Fourier coefficients have been derived for a wide variety of stars, including
Cepheids, RR Lyrae, Delta Scutis, Miras and SX Phe stars.
You may want to check the authors list for the many references to these coefficients.